லாஜிக் கதவுகளில் நாம் முக்கியமாக மற்றும் அடிப்படையாக தெரிந்து கொள்ள வேண்டிய ஒரு விதி தான். டிமார்கன் விதிகள். இந்த விதியானது பூலியன் இயற்கணிதத்தின் அடிப்படை விதிகளிலும் ஒன்றாக அறியப்படுகிறது.
மற்றபடி உள்ள இயற்கணித செயல்பாடுகளிலும் கூட, பள்ளி அளவிலேயே டிமார்கன் விதிகளை நீங்கள் படித்திருக்க வாய்ப்பிருக்கிறது. சரி எப்படி இருந்தாலும், எளிய வகையில் இந்த விதியை உங்களுக்கு விளக்கி விடுகிறேன். இந்த விதி உங்களுக்கு தெரிந்திருந்தால் தான், அடுத்தடுத்து வரக்கூடிய ஆல்ரவுண்டர் லாஜிக் கதவுகள் உங்களுக்கு எளிமையாக புரியும்.
மொத்தமாக டி மார்ன் விதிகளில் இரண்டு விதிகள் இருக்கிறது. முதலில் டிமார்கள் முதல் விதியை பார்க்கலாம்.
டிமார்கன் முதலாம் விதி
வரையறை:
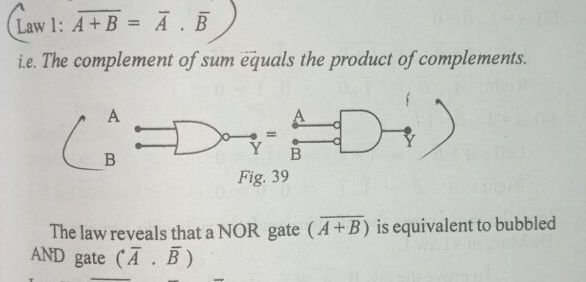
இரண்டு தர்க்க உள்ளீடுகளின் கூட்டுத்தொகையின் மறுதலை(invert value) மதிப்பானது, அந்த இரண்டு தர்க்க உள்ளீடுகளின் மறுதலை மதிப்புகளின் பெருக்கற்பலனுக்கு சமமாக இருக்கும்.
விளக்கம்:
நீங்கள் இரண்டு லாஜிக் உள்ளீடுகளை வழங்குகிறீர்கள் என வைத்துக்கொள்வோம். அந்த இரண்டு லாஜிக் உள்ளீடுகளையும் NOR கதவைக் கொண்டு லாஜிக்கல் மறுதலை கூட்டல் செயல்பாடை செய்கிறீர்கள். இதன் வெளியீடானது, இரண்டு மறுதலை லாஜிக்கல் உள்ளீடுகளின் பெருக்கல் பலனுக்கு சமமானதாக இருக்கும்.
அதற்குரிய மின்சுற்றானது படத்தில் வழங்கப்பட்டுள்ளது. இதுபோல லாஜிக் கதவுகளை ஒருங்கமைத்து நீங்களும் முயற்சி செய்து பார்க்கலாம்.
இதற்கான பூலியன் இயற்கணித உண்மை அட்டவணையானது கீழே வழங்கப்பட்டுள்ளது.

உதாரணமாக, A = 0 மற்றும் B = 0 என வைத்துக்கொள்வோம். இதன் கூட்டுத் தொகையும் 0 தான். ஆனால் இதற்கு மறு தலை எடுக்கும்போது மதிப்பு 1 ஆகிவிடும். சரி இது ஒரு புறம் இருக்கட்டும். A மற்றும் B யின் மாறுதலை மதிப்பு முறையே 1 ஆகும். இதன் பெருக்கற்பலனும் 1 தான். இப்போது புரிகிறதா?
இதுதான் டிமார்கனின் முதலாவது விதி.
டிமார்களின் இரண்டாவது விதி
டிமார்கனின் முதல் விதியை அப்படியே திருப்பி போட்டால் எப்படி இருக்குமோ! அது போல் தான் டிமார்களின் இரண்டாவது விதியும் இருக்கும். கொஞ்சம் குழப்புகிறதோ! சரி தெளிவாக சொல்கிறேன்.
வரையறை :-
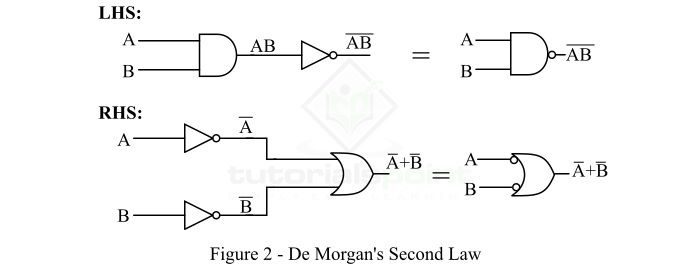
இரண்டு தர்க்க உள்ளீடுகளின் பெருக்கல் பலனின் மறுதலை மதிப்பானது, அந்த இரண்டு தர்க்க உள்ளீடுகளின் மறுதலை மதிப்புகளின் கூட்டுத்தொகைக்கு சமமாக இருக்கும்.
விளக்கம்:-
நீங்கள் இரண்டு லாஜிக் உள்ளீடுகளை வழங்குகிறீர்கள் என வைத்துக்கொள்வோம். அந்த இரண்டு உள்ளீடுகளையும் NAND கதவைக் கொண்டு லாஜிக்கல் மறுதலை பெருக்கல் செய்கிறீர்கள். இதன் வெளியீடு மதிப்பானது, உள்ளீடுகளின் தனித்தனியான மறுதலை மதிப்புகளின் கூட்டுத்தொகைக்கு சமமாக இருக்கும். இதற்கான பூலியன் இயற்கணித அட்டவணை மற்றும் மின்சுற்று படமானது கீழே வழங்கப்பட்டுள்ளது.
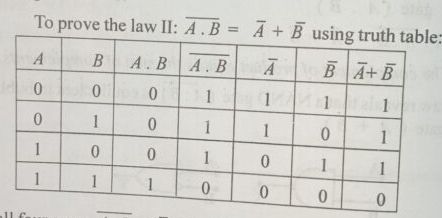
உதாரணமாக, A = 0 மற்றும் B = 0 என வைத்துக்கொள்வோம். இதன் பெருக்கு தொகையும் 0 தான். ஆனால் இதற்கு மறு தலை எடுக்கும்போது மதிப்பு 1 ஆகிவிடும். சரி இது ஒரு புறம் இருக்கட்டும். A மற்றும் B யின் மாறுதலை மதிப்பு முறையே 1 ஆகும். இதன் கூட்டுத்தொகையும் 1 தான். இப்போது புரிகிறதா?
மேற்காணும் படங்களை வைத்து உங்களுக்கு புரிந்திருக்கும் என நம்புகிறேன். புரியாவிட்டாலும் கூட, அடுத்தடுத்து வரக்கூடிய ஆல்ரவுண்டர் லாஜிக் கதவுகள் கட்டுரைகள் இதன் அடிப்படையிலேயே விளக்கங்கள் வழங்கப்படும். எனவே அதிலிருந்து எளிமையாக புரிந்து கொள்ளலாம்.
மீண்டும் ஒரு எளிய எலக்ட்ரானிக்ஸ் பகுதியில் சந்திப்போம்.
கட்டுரையாளர்:-
ஸ்ரீ காளீஸ்வரர் செ,
இளங்கலை இயற்பியல் மாணவர்,
(தென் திருவிதாங்கூர் இந்துக் கல்லூரி, நாகர்கோவில் – 02)
இளநிலை கட்டுரையாளர் மற்றும் மொழிபெயர்ப்பாளர்,
கணியம் அறக்கட்டளை.
மின்மடல் : srikaleeswarar@myyahoo.com
இணையம்: ssktamil.wordpress.com